多項式フィッティング
polyfit ファイル実行結果
実行結果は次のようになります。
うまくフィッティングできています。
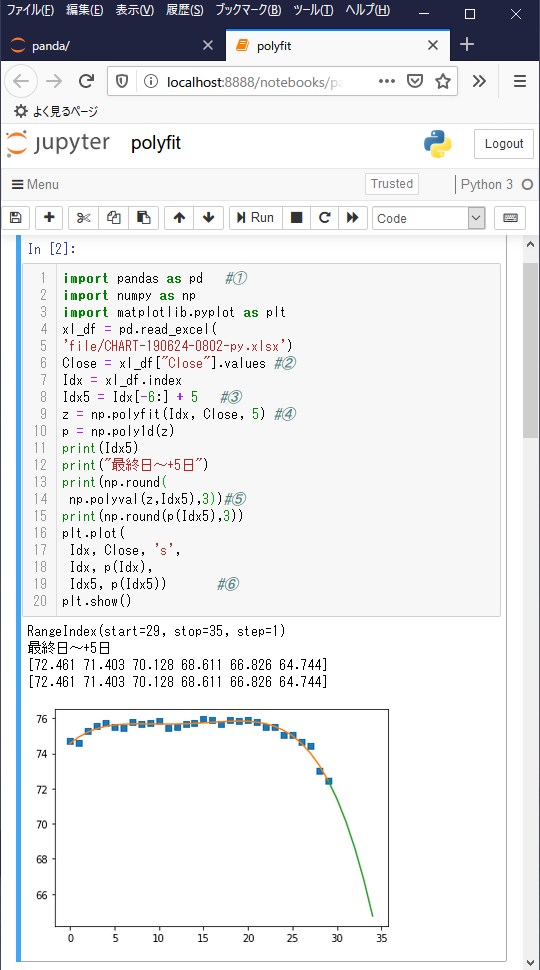
多項式フィッティングの問題点
polyfit を使うと実にうまく曲線にフィッティングできることがわかりました。
しかし、うまくフィッティングできたからといって、将来の値を予測することはできないのです。
今回の例で言えば
Idx 日付 予測値 実績
29 2019/8/2 72.461 72.459
---- ここから予測開始 ------
30 2019/8/5 71.403 71.630
31 2019/8/6 70.128 71.948
32 2019/8/7 68.611 71.823
33 2019/8/8 66.826 72.146
34 2019/8/9 64.744 71.665
となり、分かっていなかった 8/5日以降の予測値はその後判明した実績値から大きくはずれてしまいました。
ちなみに、8/2日は完璧にフィッティングできています。
でも、8/6日以降は全く予測できていません。
これを Python では「過学習」と言っているようです。
この反対は「未学習」です。
これを回避していきます。
要するに多項式の次数が大きすぎるのです。
次数を増やせばきれいにフィッティングするのですが予測はうまくいかないというジレンマに陥ります。
極大(山)/極小(谷)の数 Po と次数 N の間には次ぎの関係があります。
Po = N - 1
たとえば N = 3 とすると
極大値が1つ、極小値が1つの合計
Po = 2
となります。
ここで、polyfit ファイル実行結果の実績値■の形をざっくり見ると、極大値が1個しかなく、
次数 N は、2 とすべきことがわかります。
次数 N = 2 の時の実行結果
次数 N = 2 として実行した時の結果を示します。
④の赤丸のところを2として
z = np.polyfit(Idx, Close, 2) #④
と変更して実行しています。
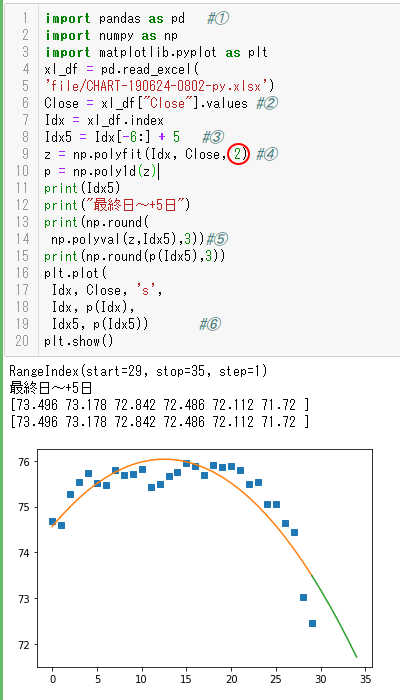
今度は、フィッティング自体はうまくできていないものの、予測は
絶対値
Idx 日付 予測値 実績 差分
29 8/2 73.496 72.459
---- ここから予測開始 ------
30 8/5 73.178 71.630 1.5
31 8/6 72.842 71.948 0.9
32 8/7 72.486 71.823 0.7
33 8/8 72.112 72.146 0.0
34 8/9 71.720 71.665 0.0
差分絶対値合計 3.1
となり、8/2~8/7 は、ずれてはいるものの 8/8日以降の予測値は
その後判明した実績値に近いことがわかります。
このあと、このフィッティング関数 np.polyfit() の問題点をさらに検証していきたいと思います。
長くなりましたのでここで一旦切りたいと思います。
多項式フィッティングの問題点その2 に続く
polyfit ファイル作成準備その2 に戻る
Python 多項式フィッティング概要 に戻る